Ре­ше­ние.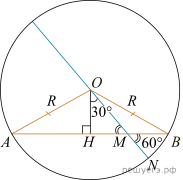

Обо­зна­чим концы хорды А и В, центр окруж­но­сти  — О. Про­ве­дем ра­ди­у­сы OA и OB, в тре­уголь­ни­ке AOB про­ве­дем вы­со­ту OH. Тре­уголь­ник AOB  — рав­но­бед­рен­ный, по­это­му OH  — ме­ди­а­на, AH  =  HB. Длина хорды AB равна 2 + 12  =  14, тогда AH  =  7. По тео­ре­ме Пи­фа­го­ра в тре­уголь­ни­ке AOH:

Пусть M  — точка пе­ре­се­че­ния диа­мет­ра окруж­но­сти и хорды AB. Угол HMO равен 60°, по­это­му угол HOM равен 30°. Тогда а зна­чит, 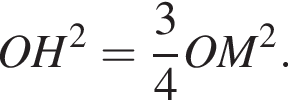Сле­до­ва­тель­но,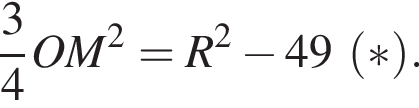

По свой­ству пе­ре­се­ка­ю­щих­ся хорд от­ку­да Под­став­ляя в (⁎), по­лу­ча­ем:

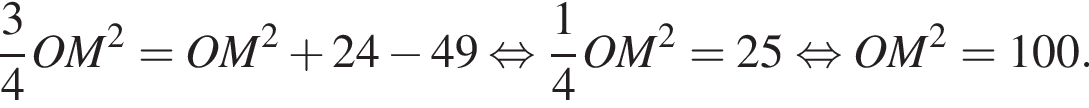
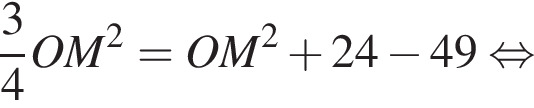
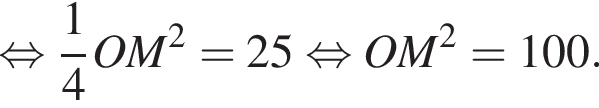
Тогда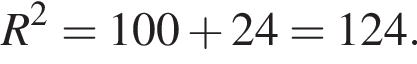

Ответ: 124.